Matrix Calculus Notes

Table of Contents

矩阵求导的一些笔记。

单变量求导规则(Scalar derivative rules)

Basic rules of derivatives

设 $y = f(u)$，$u = g(x)$，那么 $y = f(g(x))$ 。

则 $y$ 关于 $x$ 的导数可以用链式法则来求出：

$$\frac{\partial{y}}{\partial{x}} = \frac{\partial{y}}{\partial{u}} \frac{\partial{u}}{\partial{x}}$$

对于 $f(x, y) = 3 x^2 y$，分别对自变量 x, y 求导，则得到了 $f(x, y)$ 的梯度（gradient）：

$$ \nabla{f}(x, y) = [\frac{\partial f}{\partial x}, \frac{\partial f}{\partial x}] = [6xy, 3x^2] $$

设自变量为

$$ \mathbf{x} = \left[ \begin{array} \
x_1 \\
x_2 \\
... \\
x_n
\end{array} \right] $$

因变量为

$$ \mathbf{y} = \left[ \begin{array} \
y_1 \\
y_2 \\
... \\
y_m
\end{array} \right] $$

且

$$ y_1 = f_1(\mathbf{x}) \\
y_2 = f_2(\mathbf{x}) \\
... \\
y_m = f_m(\mathbf{x})
$$

定义 y 关于 x 的导数为 y 关于 x 的 Jacobian 矩阵：

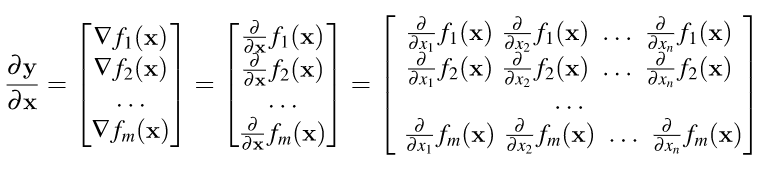
Jacobian matrix

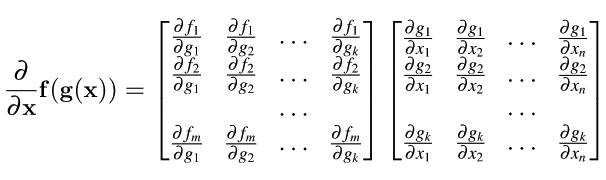
Matrix chain rule

注意矩阵乘法不具有交换性。